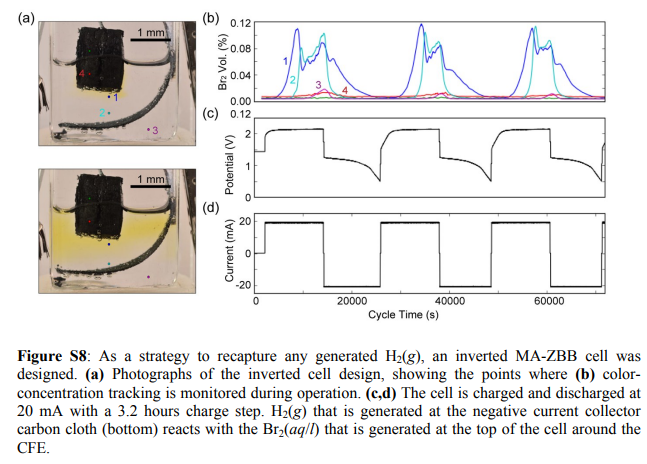
Earlier this month, I wrote an article about the use of non-aqueous solvents in Zn-Br batteries. The only published result I could find was an article dealing with Zn-Br flow batteries using propionitrile as the catholyte solvent but I wanted to avoid the use of propionitrile due to its toxicity and scarcity (hard to find/buy for an individual in the US). However I thought propylene carbonate (PC) could be a suitable replacement, so I bought some to test whether this was true or not.
The first experiments I carried out were to figure out whether PC could be used as the sole solvent within the battery. Sadly the solubility of ZnBr2 is not high enough – at most in the 0.5-1M range at 20C – and the conductivity of these ZnBr2 solutions was also not high enough, with very noisy charge/discharge curves with very high charge voltages that retained almost no charge at all.
The solubility of both TMPhABr and TBABr in PC is better, although TBABr is by far the most soluble. With TBABr I was able to achieve saturated solutions with almost 50% of TBABr, giving them a very decent amount of conductivity. Sadly this wasn’t enough to make PC usable as a single electrolyte though, as the bad behavior of the charge/discharge was also apparent when using this as the sole solvent.
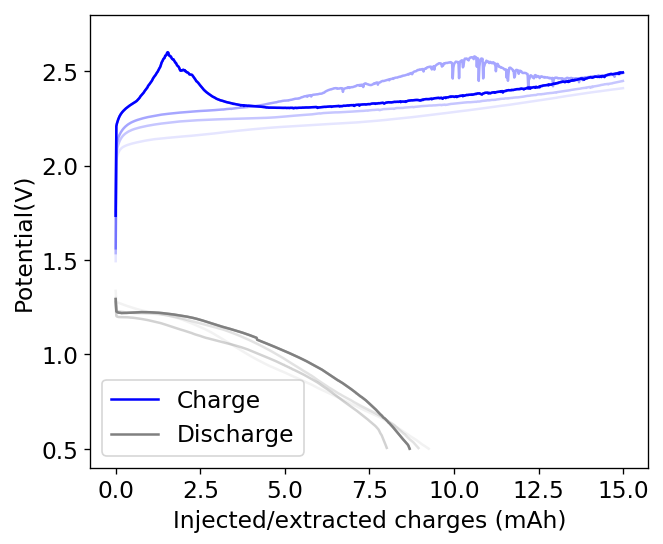
The idea then came to use this concentrated PC TBABr solution to saturate the GFE-1 cathode and use this in an inverted cell. It is interesting that although PC is infinitely miscible with water, a 50% solution of PC TBABr is actually not miscible with a 1.5M ZnBr2 solution in water. This is because the affinity of TBABr for PC is much higher than that of ZnBr2 and the affinity of ZnBr2 for water is also significantly higher as well.
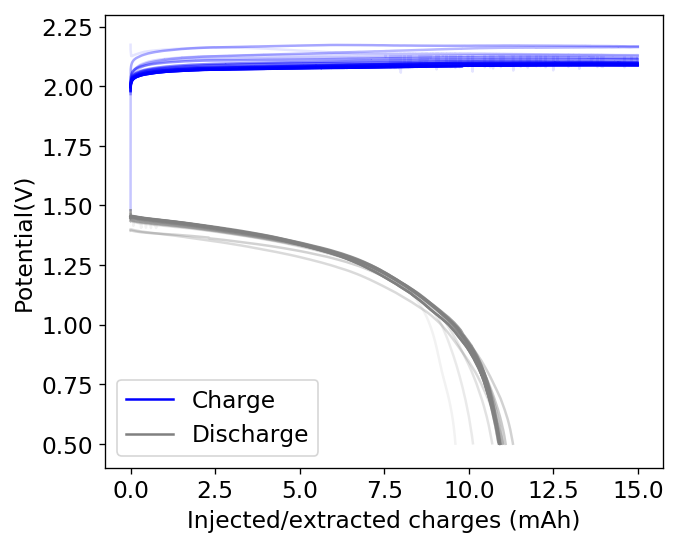
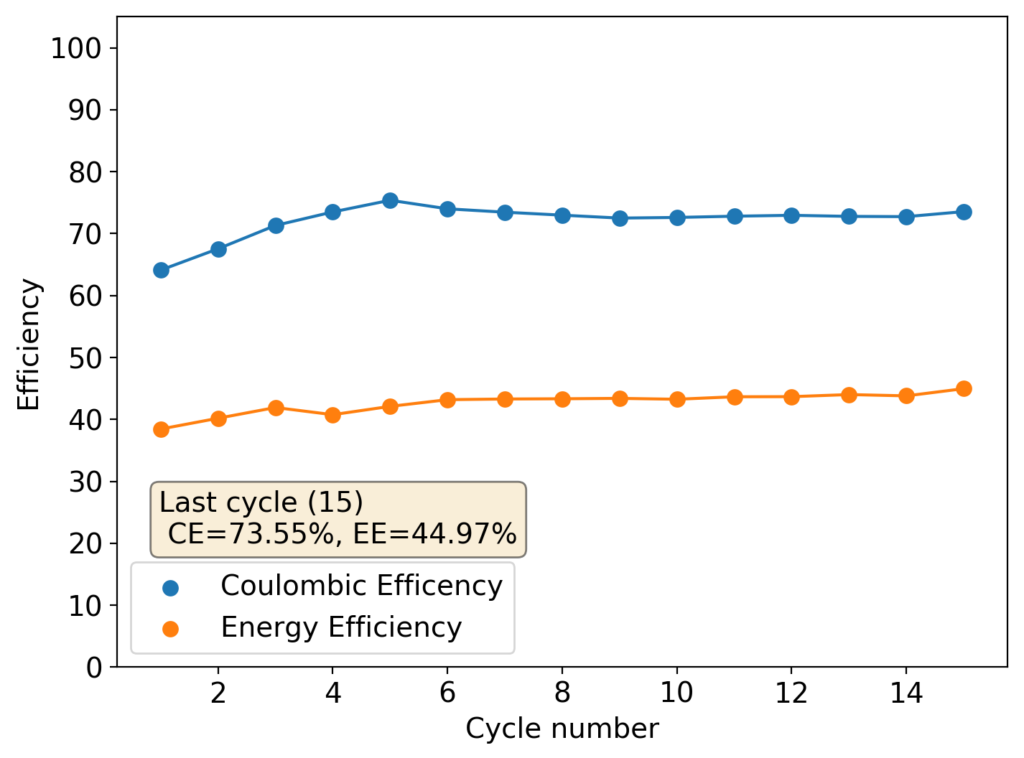
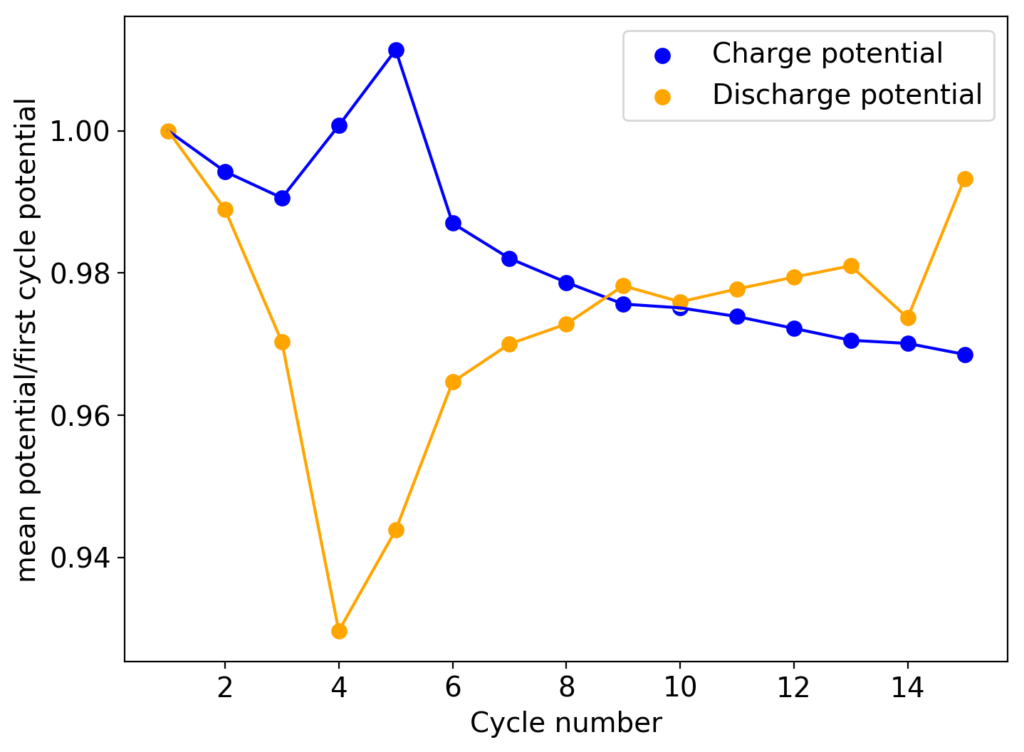
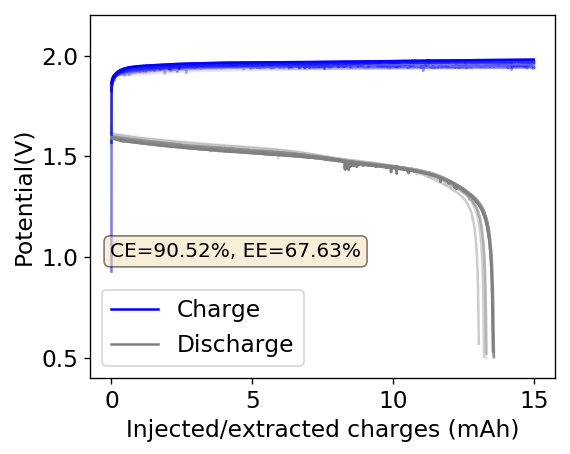
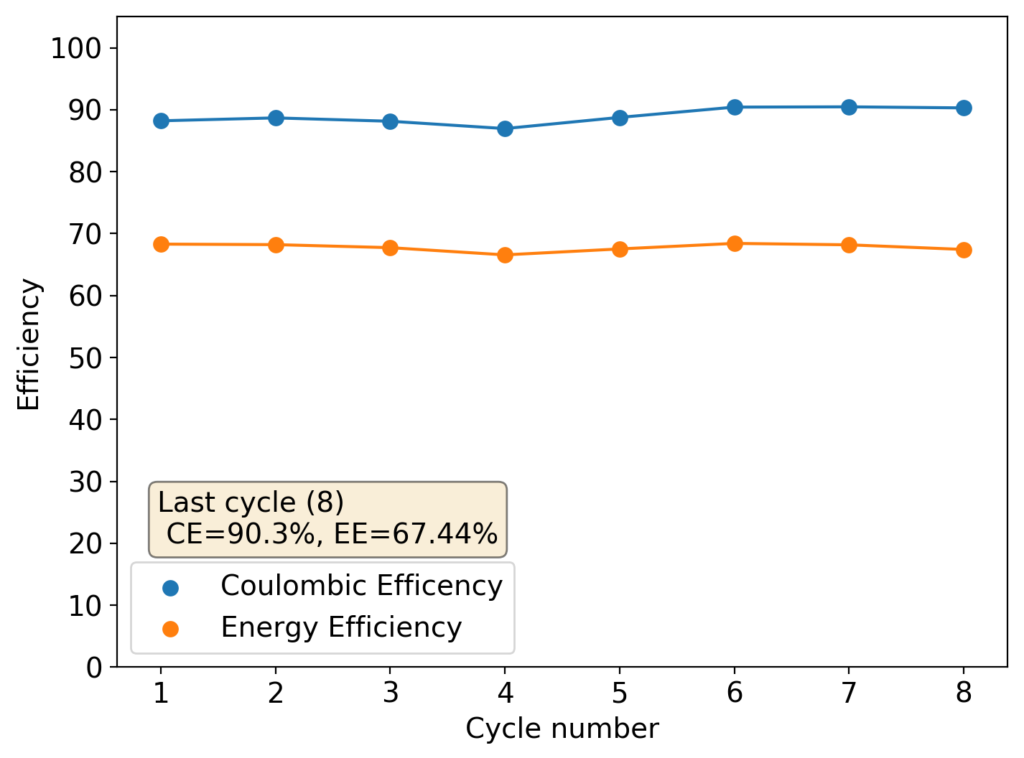
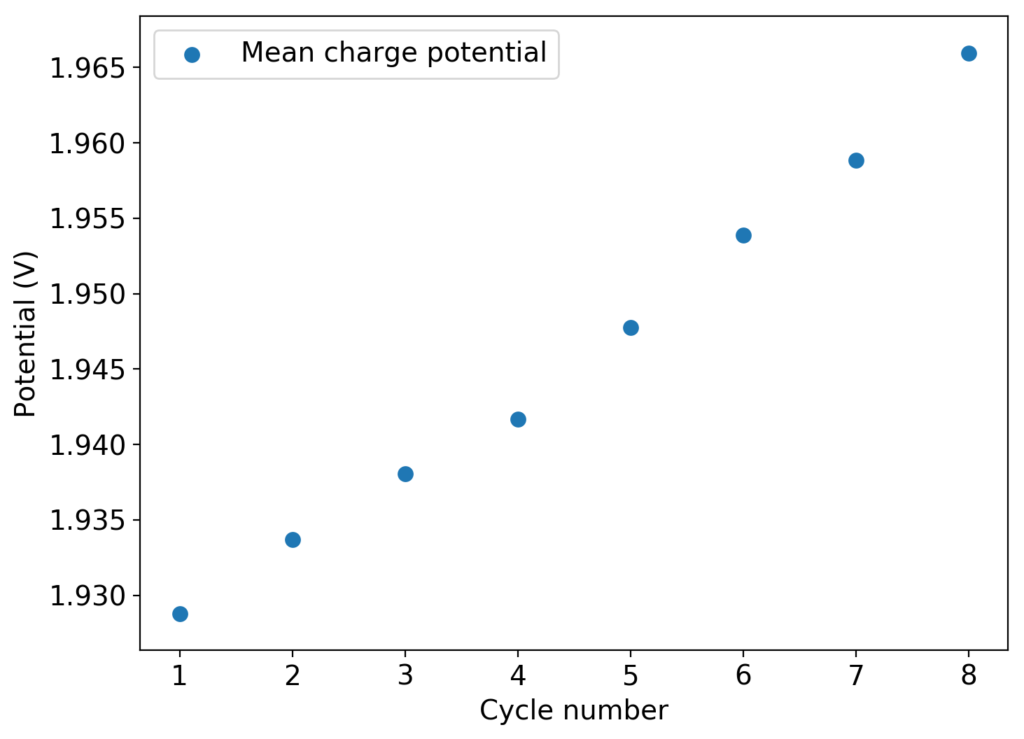
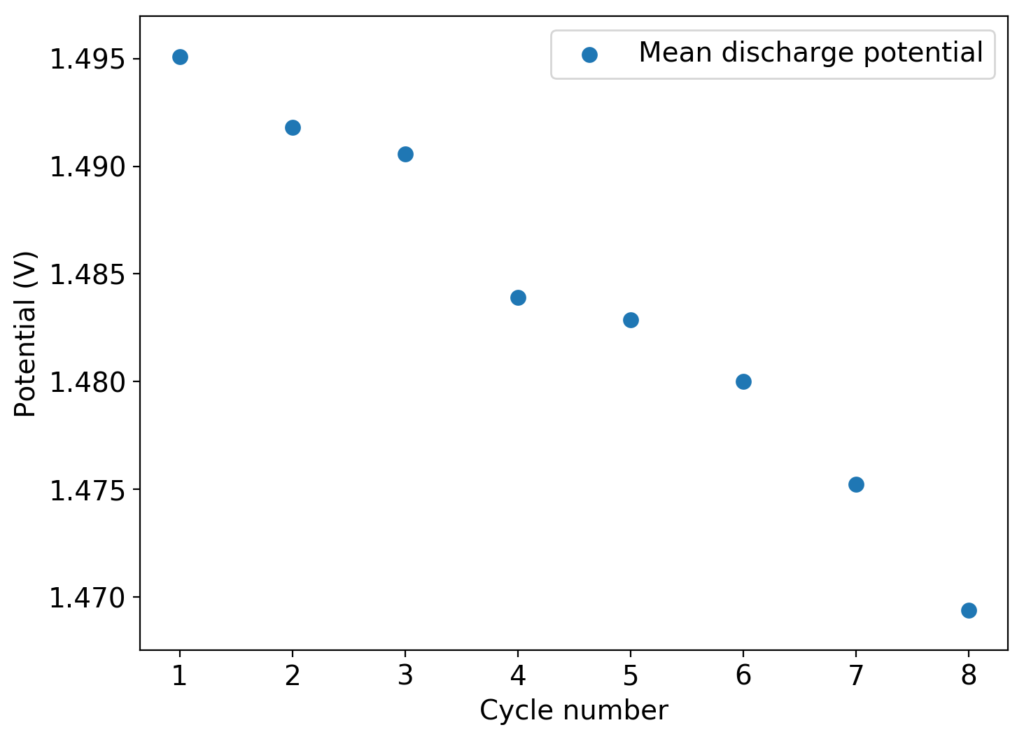
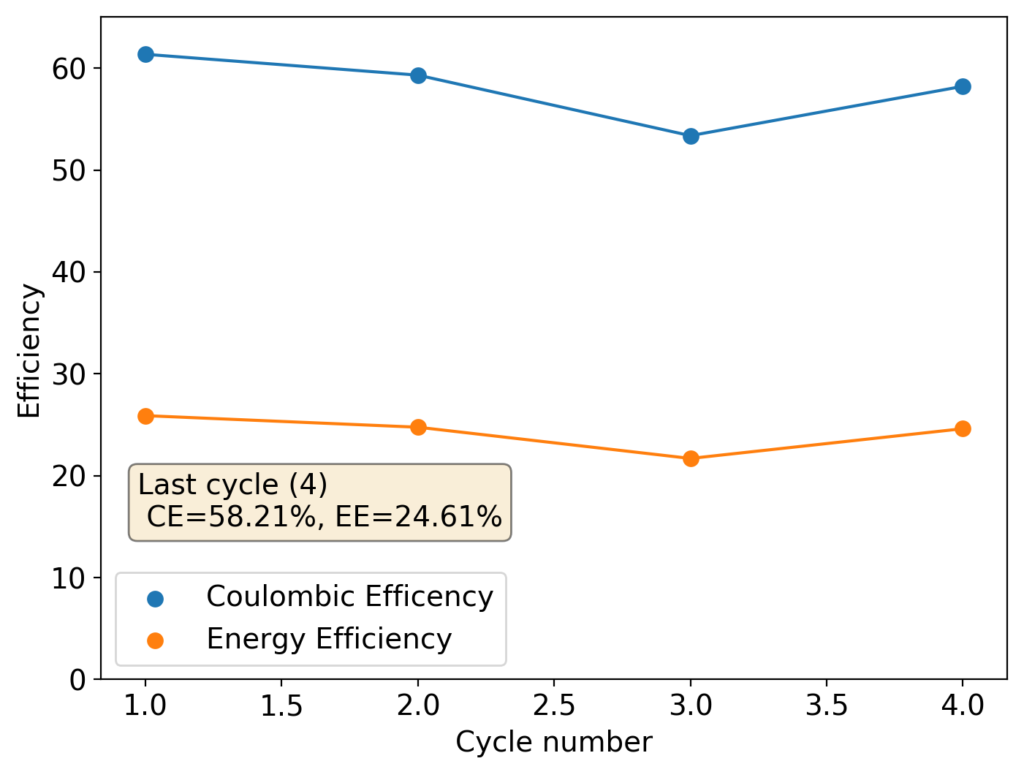
This experiment was better behaved with actually measurable charge/discharge curves. I did 4 curves charging/discharging to 15mAh at 15mA – the results are shown above – with the best CE and EE values being 61% and 25% respectively. The charging voltages do show that the internal resistance is significantly higher than when using water so there is likely a lot more of hydrogen evolution at the anode. The generation of elemental bromine at the cathode is also probably significantly slower, given the much higher viscosity and lower conductivity of the PC electrolyte.
Given the higher charge density used, I thought It might be the case that the PC electrolyte is just not able to support as high of a current density as the normal aqueous electrolyte and therefore a much lower charge density needs to be used to use this successfully. I am going to be evaluating this hypothesis within my next few tests.